BUAACT-Chap07-源程序的中间形式

第七章 源程序的中间形式

7.1 波兰表示

7.1.1 表达式的波兰表示

例：赋值语句的波兰表示：

    A := F * 3.1416 * R * (H + R)
=>  A F 3.146 * R * H R + * :=

由中缀表达式翻译为波兰表示算法：

设一个操作符栈；当读到操作数时，立即输出该操作数，当扫描到操作符时，与栈顶操作符比较优先级，若栈顶操作符优先级高于栈外，则输出该栈顶操作符；反之，则栈外操作符入栈。

波兰表示法的优点： - 在不使用括号的情况下可以无二义地说明算术表达式； - 波兰表示法更容易转换成机器的汇编语言或机器语言，操作数出现在紧靠操作符的左边，而操作符在波兰表示中的顺序即为进行计算的顺序。 - 波兰表示不仅能用来作为算术表达式的中间代码形式，而且也能作为其它语言结构的中间代码形式。

7.1.2 if 语句的波兰表示

    if <expr> then <stmt1> else <stmt2>
=>  <expr> <label1> BZ <stmt1> <label2> BR <stmt2>

• <label1>位于BR与<stmt2>之间，<label2>位于<stmt2>之后。
• BZ：二目操作符，如果<expr>的计算结果为0（false），则产生一个<label1>的转移；
• BR：一目操作符，它产生一个<label2>的转移。

其它语言结构也很容易将其翻译成波兰表示，但使用波兰表示优化不是十分方便。

7.2 N-元表示

在该表示中，每条指令由 n 个域所组成，通常第一个域表示操作符，其余为操作数。常用的 n 元表示是：三元式、四元式。

7.2.1 三元式

操作符	左操作数	右操作数

表达式的三元式的例子：

w * x + (y + z)

转化为：

*,  w ,  x
+,  y ,  z
+, (1), (2)

第三个三元式中的操作数(1)、(2)表示 (1) 和 (2)两条三元式的计算结果。

条件语句的三元式：

If x > y then
    z := x;
else z := y + 1;

转化为：

 - ,  x ,  y
BMZ, (1), (5)
:= ,  z ,  x
BR ,    , (7)
 + ,  y ,  1
:= ,  z , (5)

• BMZ：是二元操作符，测试第二个域的值。若小于等于 0，则按第 3 个域的地址转移，若为正值则该指令作废；
• BR：一元操作符，按第 3 个域作无条件转移。

使用三元式也不便于代码优化，为了便于在三元式上作优化处理，可使用间接三元式。

7.2.2 间接三元式

A := B + C * D / E
F := C * D

用直接三元式表示为：

* ,  C ,  D
/ , (1),  E
+ ,  B , (2) 
:=,  A , (3)
* ,  C ,  D 
:=,  F , (5)

优化掉(5)式后：

* ,  C ,  D
/ , (1),  E
+ ,  B , (2) 
:=,  A , (3)
:=,  F , (1)

间接三元式将执行次序与三元式编号分离：

* ,  C ,  D
/ , (1),  E
+ ,  B , (2) 
:=,  A , (3)
:=,  F , (1)

操作：(1)、(2)、(3)、(4)、(1)、(5)

三元式的执行次序用另一张表表示，这样在优化时（三元式位置的变更实际是执行顺序的变化），三元式可以不变，而仅仅改变其执行顺序表。

7.2.3 四元式

操作符	左操作数	右操作数	结果

结果：通常是编译时分配的临时变量，可由编译程序分配一个寄存器或主存单元。

例：

(A + B) * (C + D) - E

转化为四元式：

+,  A,  B, T1
+,  C,  D, T2
*, T1, T2, T3
–, T3,  E, T4

其中T1~T4为临时变量。

用四元式优化比较方便。

7.3 抽象机代码

许多 Pascal 编译系统生成的中间代码是一种称为 P-code 的抽象代码。P-code 中的“P”即“Pseudo”。

“抽象机”是虚拟的一台“堆栈计算机”。该堆栈式计算机主要由若干寄存器、一个保存程序指令的储存器和一个堆栈式数据及操作存储组成。

寄存器有：

寄存器名	用途
PC	程序计数器
NP	New 指针，指向“堆”的顶部。“堆”用来存放由 New 生成的动态数据
SP	运行栈指针，存放所有可按源程序的数据声明直接寻址的数据
BP	基地址指针，即指向当前活动记录的起始位置指针
其他	如 MP-栈标志指针，EP-极限栈指针

计算机的储存

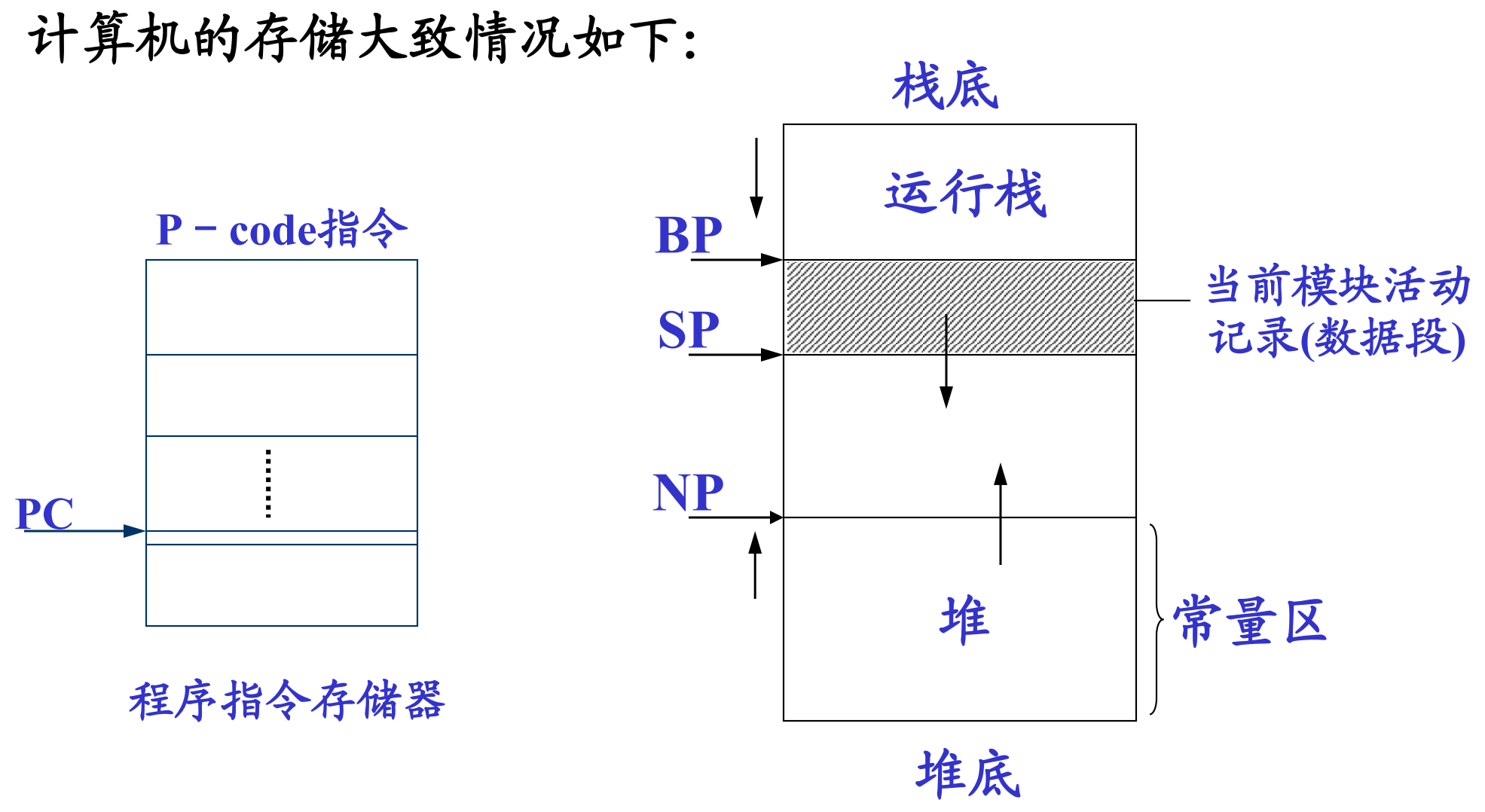
运行P– code的抽象机没有专门的运算器或累加器，所有的运算（操作）都在运行栈的栈顶进行，如要进行d := (a + b) * c的运算，生成P– code序列为：

LOD a  # a 入栈
LOD b  # b 入栈
ADD    # 弹出两个元素相加，结果入栈
LOD c  # c 入栈
MUL    # 弹出两个元素相乘，结果入栈
STO d  # 弹出栈顶，赋值给 d

7.4 其它形式的中间代码

7.4.1 抽象语法树（AST: Abstract Syntax Tree）

用树形图的方式表示中间代码，操作数出现在叶节点上，操作符出现在中间结点上。例如：(A + B * C) / (D * E - (F＋ G) / (H + I))

抽象语法树

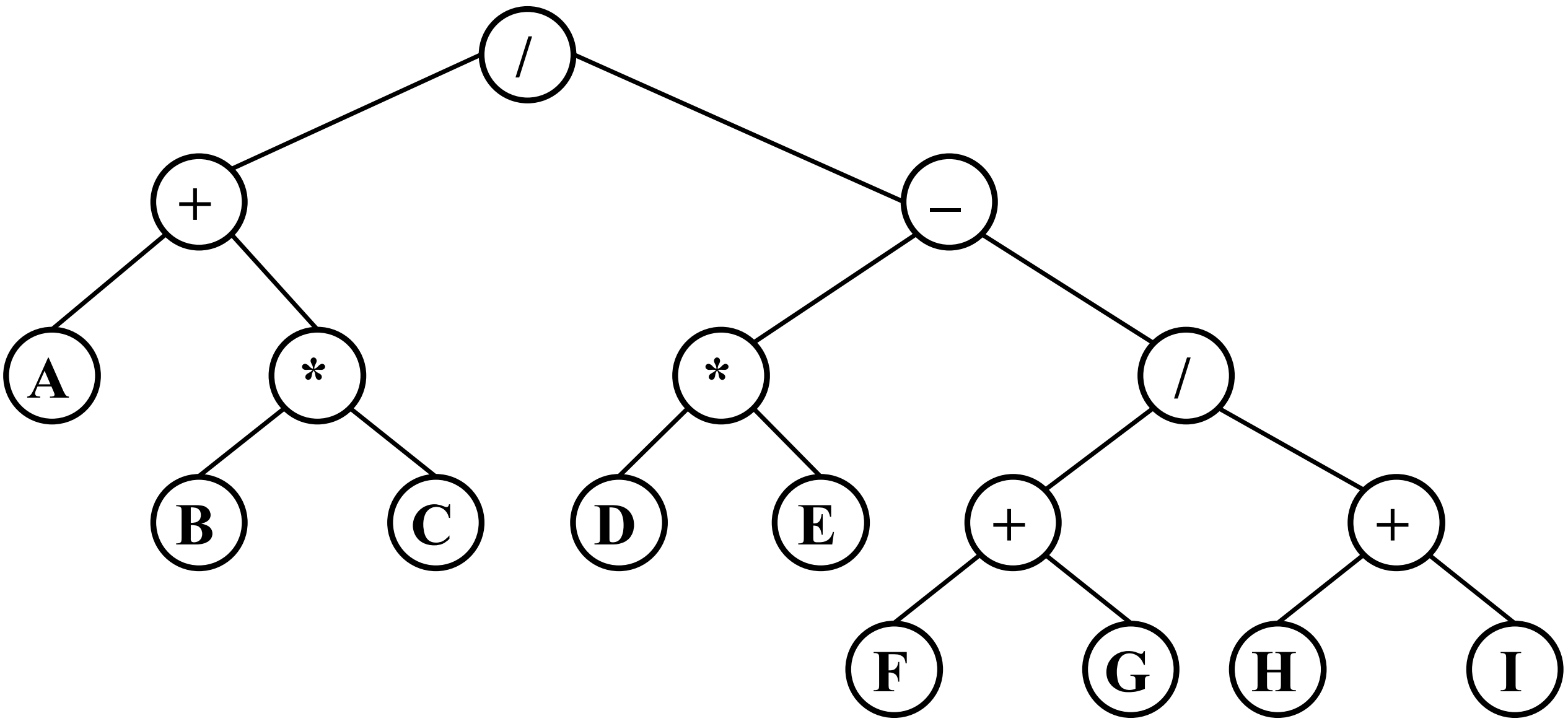
7.4.2 DAG图（Directed Acyclic Graphs 有向无环图）

语法树的一种归约表达方式：

• 图的叶节点由变量名或常量所标记。对于那些在基本块内先引用再赋值的变量，可以采用变量名加下标0的方式命名其初值；
• 图的中间节点由中间代码的操作符所标记，代表着基本块中一条或多条中间代码；
• 基本块中变量的最终计算结果，都对应着图中的一个节点；具有初值的变量，其初值和最终值可以分别对应不同的节点。

例如赋值语句：a = b * (-c) + b * (-c)

DAG图的例子

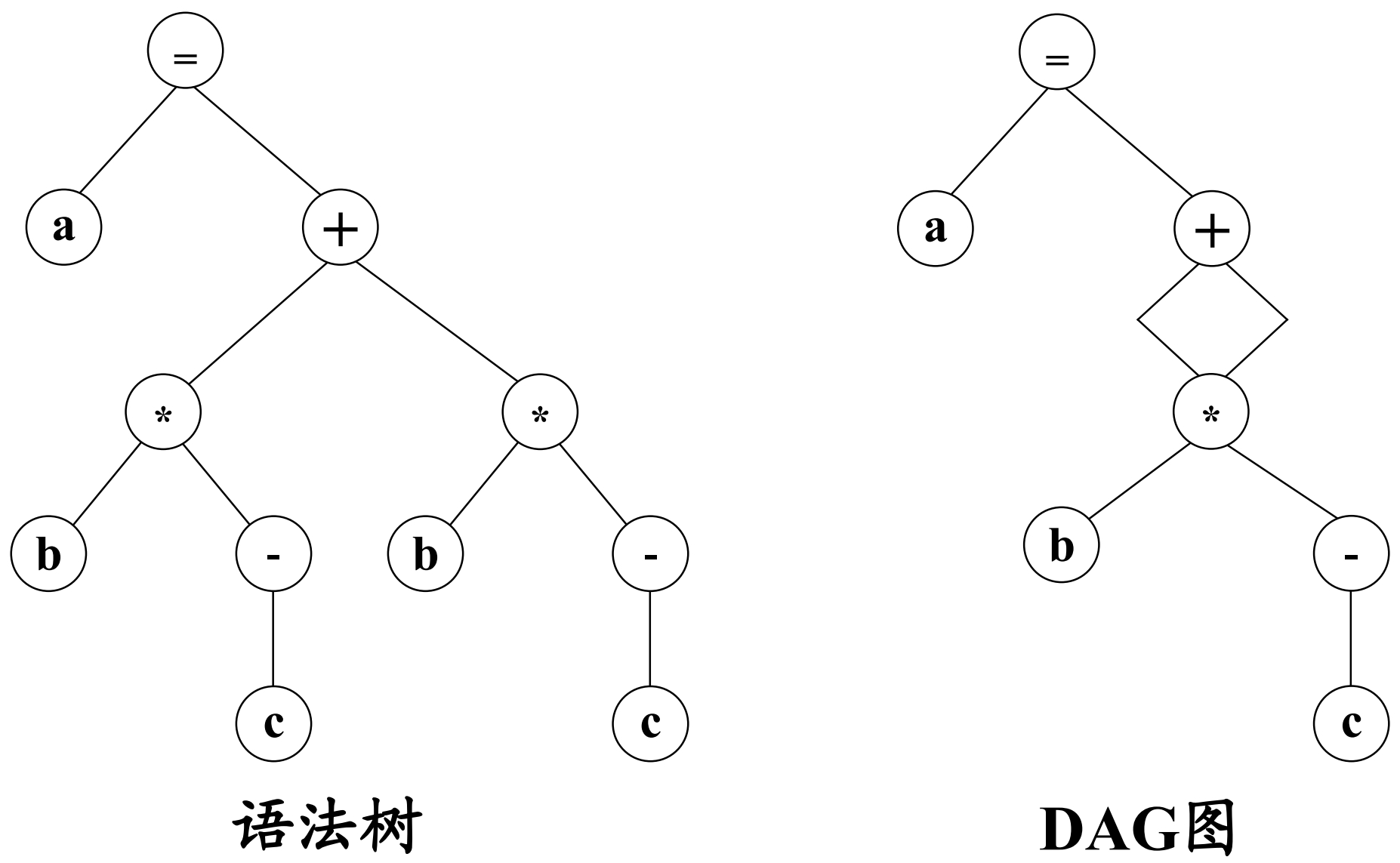
7.4.5 一种特殊的四元式表达方式：SSA

Single Static Assignment form（SSA form）静态单一赋值形式的 IR，主要特征是每个变量只赋值一次。

SSA 的优点：

• 可以简化很多优化的过程；
• 可以获得更好的优化结果。

从四元式到 SSA 的转化：

四元式到SSA的转化

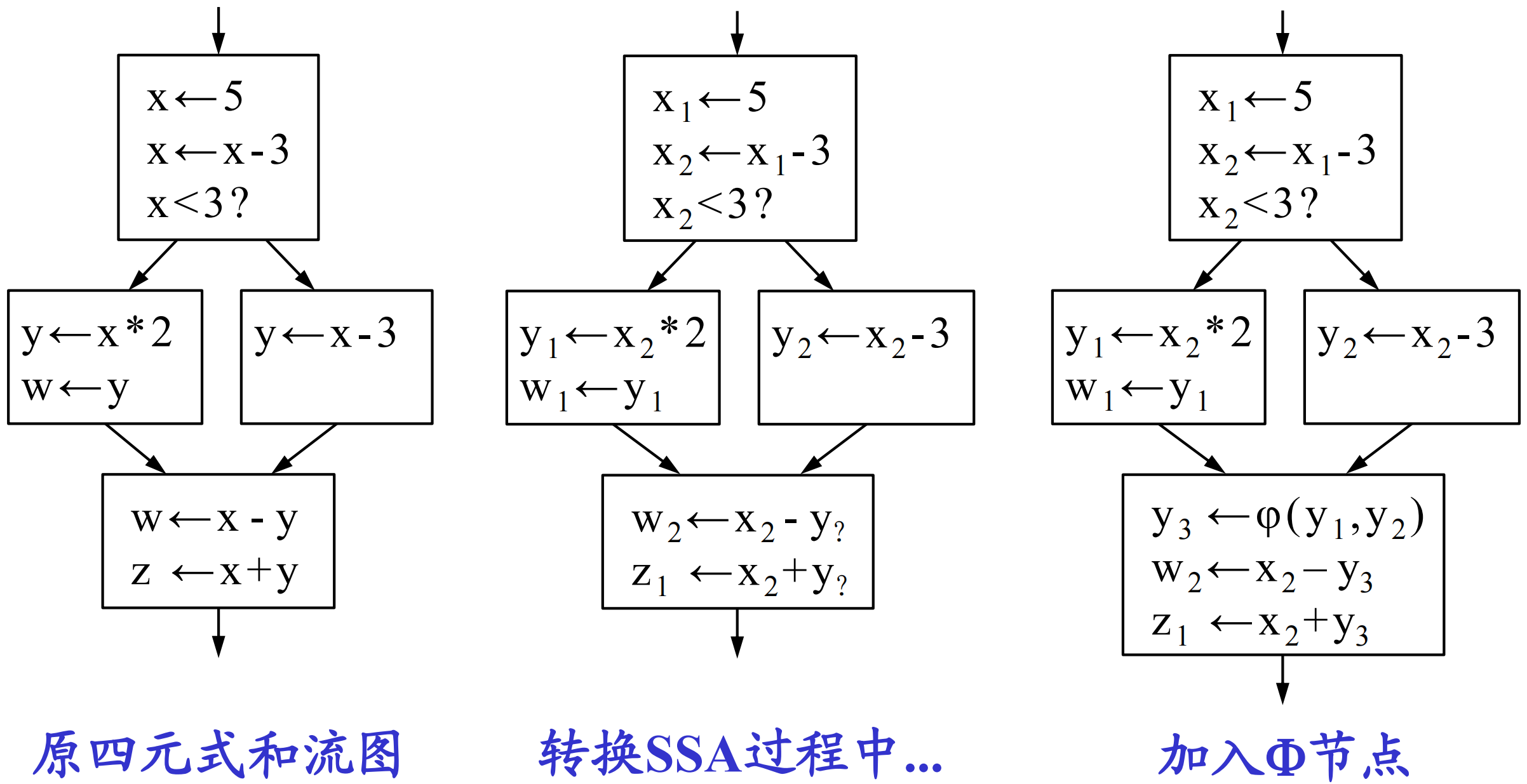
SSA 的关键问题——如何加入 \(\varphi\) 结点？

\(\varphi\) 节点的参数应包括所有可能到达其位置的同一个变量的所有定义：\(x_{n+1} = \varphi(x_1, x_2,..., x_n)\)。

在某个分支汇聚点，如果有同一个变量的多个定义点可能到达，就需要在此处增加相应的 \(\varphi\) 结点，汇聚所有可能到达的定义，将其转化为新的定义。