BUAACT-Chap10-语义分析和代码生成

第十章 语义分析和代码生成

本章假设：

• 源语言：通用的过程语言（不是面向对象的语言）
• 生成代码：栈式抽象机的（伪）汇编程序 P-code
• 翻译方法：自顶向下的属性翻译
• 语法成分翻译子程序的参数设置：
  • 继承属性为值形参
  • 综合属性为变量形参
• 语法成分翻译动作子程序的参数设置：
  • 继承属性为值形参
  • 综合属性不设形参，而作为动作子程序的返回值（由 RETURN语句返回）

10.1 语义分析的概念

1. 上下文有关分析：即标识符的作用域
2. 类型的一致性检查
3. 语义处理：
   • 声明语句：其语义是声明变量的类型等，并不要求做其他的操作。语义分析程序的工作是填符号表，登录名字的特征信息，分配存储。
   • 执行语句：语义是要做某种操作（其中包含查询符号表以检查变量是否在作用域中）。语义处理的任务：按某种操作的目标结构生成中间代码或目标代码。

用上下文无关文法只能描述语言的语法结构，而不能描述其语义！此时最好采用上下文相关文法进行描述。

例如在对标识符进行操作前需要检查所在块（BLOCK）内含有标识符的声明，因此这是上下文有关的。

而实际上上下文有关分析实现起来难度大，因此通常使用符号表来检查的程序中的语义是否正确。

10.2 栈式抽象机及其汇编指令

栈式抽象机：由三个存储器、一个指令寄存器和多个地址寄存器组成。

存储器：

• 数据存储器（存放 AR 的运行栈）
• 操作存储器（操作数栈）
• 指令存储器

计算机的存储结构

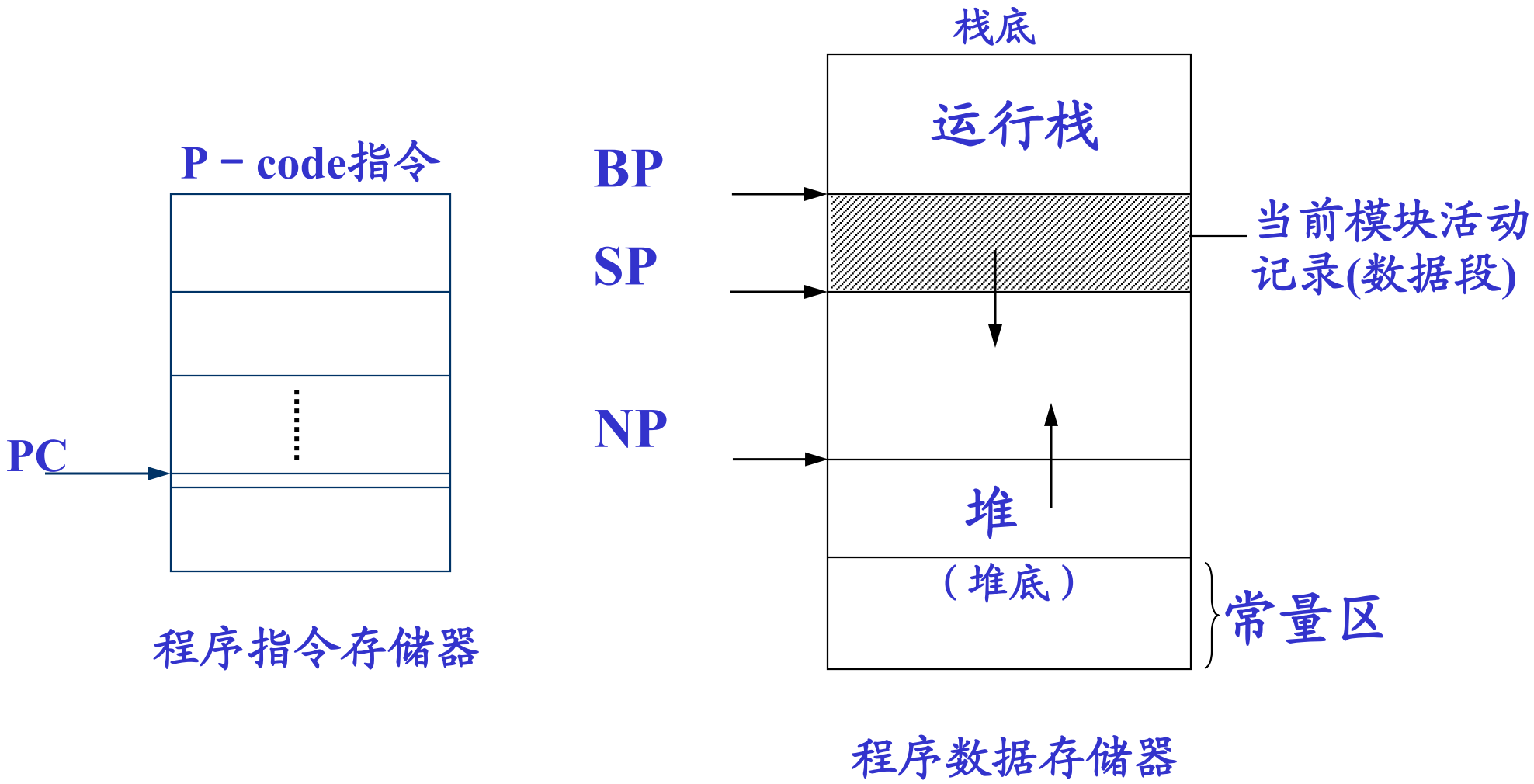
实际上的电脑中，栈区一般只占很小的一部分，而堆的容量巨大。这个概念一定要有，否则你的水平等同于北大青鸟。

——邵兵

对于a := b + c语句，其 P-code 指令如下：

LDA (a)
LOD b
LOD c
ADD
STN

栈式抽象机指令代码如下：

指令名称	操作码	地址	指令意义
加载指令	LOD	D	将 D 入栈
立即加载	LDC	常量	将常量入栈
地址加载	LDA	(D)	将 D 的地址入栈
存储	STO	D	弹栈并将结果存入 D
间接存	ST	@D	弹栈并将结果存入 D 所指单元
间接存	STN		弹栈两次，将栈顶存入次栈顶所指单元
加	ADD		弹栈两次，加和入栈
减	SUB		弹栈两次，次栈顶减去栈顶，结果入栈
乘	MUL		弹栈两次，结果乘积入栈
等于比较	EQL		弹栈两次，次栈顶与栈顶比较，结果（1 或 0）入栈
不等于比较	NEQ
大于比较	GRT
小于比较	LES
大于等于	GTE
小于等于	LSE
逻辑与	AND		弹栈两次，栈顶与次栈顶运算，结果入栈
逻辑或	ORL
逻辑非	NOT
转子	JSR	lab	程序跳转到行号 lab 处
分配	ALC	M	在运行栈顶分配大小为 M 的活动记录区

10.3 声明的处理

语义表示

给出语言结构的属性翻译文法来说明其语义及语义动作，并把这些语义动作插入属性翻译文法产生式中的适当位置。

编译程序的任务

编译程序处理声明语句要完成的主要任务

1. 分离出每一个被声明的实体，并把它们的名字填入符号表中；
2. 把被声明实体的有关特性信息尽可能多地填入符号表中。

对于已声明的实体，在处理该实体的引用时要做的事情

1. 检查对所声明的实体引用（种类、类型等）是否正确；
2. 根据实体的特征信息，例如类型、所分配的目标代码地址（可能为数据区单元地址，或目标程序入口地址）生成相应的目标代码。

也就是说，处理声明语句主要是做填表工作（填表前先得查表，检查是否重名）。

处理对已声明的实体的引用时主要是做查表工作。

声明的两种方式

1. 类型说明符放在变量的前面。如C语言：int a;。在填表时已知类型和a的值（名字），直接填入符号表。
2. 类型说明放符在变量的后面。如：Pascal，PL/1，Ada等，需要返填。

10.3.1 常量类型声明的处理

常量标识符通常被看做是全局名，是在堆中分配空间，如：

const int a = 3;

常量声明的 ATG 如下：

常量声明的ATG

@inser的功能是：

• 检查声明的类型t和常量表达式的类型s是否一致，若不一致，则输出错误信息；
• 把名字n，类型t和常量表达式的值c填入全局符号表中。

10.3.2 简单变量声明处理

ATG 文法：

简单变量的声明

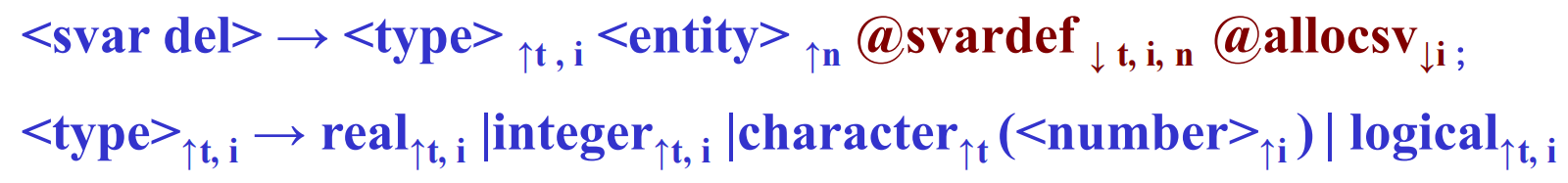
其中：

• n：变量名；
• t：变量类型；
• i：该类型变量所需数据空间的大小。

@svardef动作符号是把n、i和t填入符号表中：

procedure svardef(t, i, n);
	j := tableinsert(n, t, i);    // 将有关信息填入符号表
	if j = 0                      // 填表时检查是否重名
		then errmsg(duplicate, statementno);
	else if j = -1                // 符号表已满
		then errmsg(tblovflow, statementno);
		abort;                    // 符号表溢出，编译终止
end svardef;

@allicsv为简单变量分配数据空间

procedure allocsv(i);
	codeptr := codeptr + i; //codeptr 为地址区指针
end allocsv;

@svardef和@allocsv可以合并。

10.3.3 数组变量的声明处理

对于静态数组，即数组的大小在编译时是已知的，编译程序在处理数组声明时，可建立一个数组模板（又称为数组信息向量）以便以后的程序中引用该数组元素时，可按照该模板提供的信息，计算数组元素（下标变量）的存储地址。

对于动态数组，其大小只有在运行时才能最后确定。我们在编译时仅为该模板分配一个空间，而模板本身的内容将在运行时才能填入。

数组声明的 ATG 文法（例如array B(N, -2: 1) char;）

数组声明的ATG文法

@init的功能为在分配给数组模板区中保留两个存储单元，用来放 RC 和 n，并将维数计数器 j 清0；

数组模板

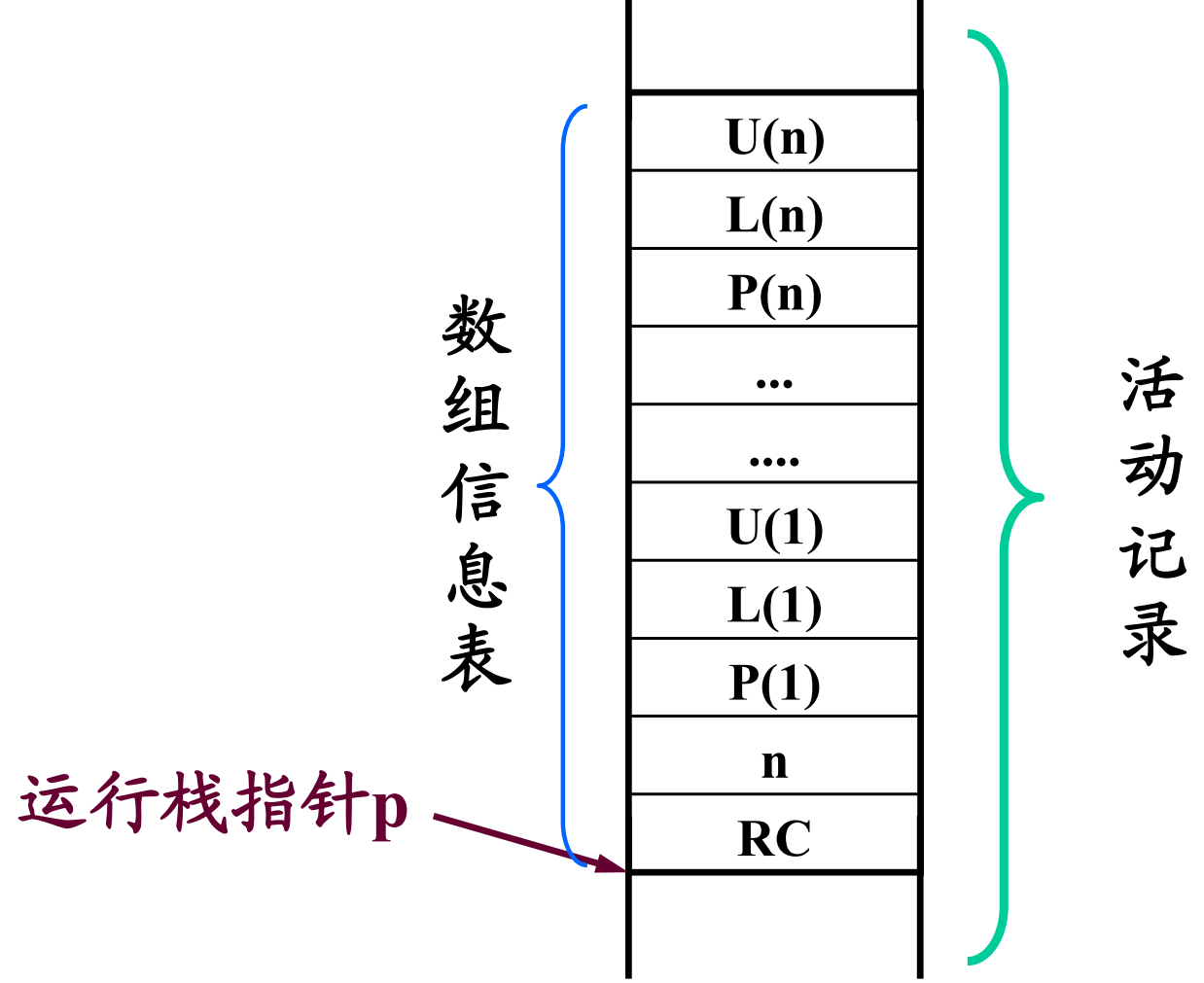
@dimen#：j := j + 1，即统计维数；

@bannds：将省略下界表达式情况的u => U(i)，但应把相应的L(i)置成隐含值 1，然后计算P(i)；

实际上P(i)的计算公式：

• P(n) = 1；
• P(i) = [U(i + 1) - L(i + 1)] * P(i + 1)。

@lowerbnd：生成l => L(i)的代码；

@upperbnd：生成u => U(i)的代码，计算P(i)，并将P(i)的值送至模板区。

最后的动作程序@symbinsert是把数组名n，数组维数j和数组元素类型t及数组标志k填入符号表中，为数组分配存储空间。

10.4 表达式的处理

分析表达式的主要目的是生成计算该表达式值的代码。通常的做法是把表达式中的操作数装载（LOAD）到操作数栈（或运行栈）栈顶单元或某个寄存器中，然后执行表达式所指定的操作，而操作的结果保留在栈顶或寄存器中。

整形表达式的 ATG 文法：

整形表达式的ATG文法

procedure lookup(n);
	string n; integer j;
	j:= symblookup(n); // 名字n表项在符号表中的位置
	if j < 1 then error();
	else return(j);
end;

procedure push(j);
	integer j;
	emit("LOD", symbtbl(j).objaddr);
end;

procedure pushi(i); /*压入整数*/
	integer i;
	emit("LDC", i) ;
end;